“Dios algunas veces geometriza”, Platón (427-347 a. C.)
Phi (Φ,φ) -el número áureo, de oro o de Fibonacci- es un concepto de sobra conocido y estudiado por matemáticos de todos los tiempos, pero que a su vez, tampoco es del todo ajeno para los amantes del arte, la biología, la arquitectura, la música, la botánica o las finanzas, por ejemplo. No es difícil que se hayan tropezado con él en cualquiera de estas disciplinas. ¿Significa esto que es posible entonces encontrar una traducción numérica para todo lo que vemos, oímos o construimos a nuestro alrededor? Quizás la respuesta más cercana que podamos dar a esta pregunta sea la frase de Platón que abre este artículo.
Sin embargo, sí podemos indagar en un fenómeno matemático que ha atraído la atención de pensadores de todas las disciplinas y épocas desde que fuera descubierto: la proporción áurea o la divina proporción. Para entrar en materia tenemos que remontarnos a la historia del matemático Leornardo Bigollo (Leonardo Pisano o de Pisa), Fibonacci.
La espiral de Fibonacci
Phi (Φ,φ) se llama Phi gracias al famoso escultor griego Fidias (siglo 5 a. C.), autor de grandes hitos arquitectónicos como el Partenón de Atenas. Según cuenta Mario Livio en su libro “La proporción áurea: La historia de Phi, el número más sorprendente del mundo”, ciertos historiadores sostenían que Fidias habría utilizado con esmero la proporción áurea en sus obras. Fue por eso que el matemático estadounidense Mark Barr decidió honrarle nombrando a Φ con su inicial en griego (Phi). Es decir, Phi, ni fue descubierto por Fibonacci (había sido ya definido y estudiado por Euclides), ni debe su nombre al italiano. Dicho esto, sin embargo, es preciso acudir al hallazgo del italiano para adentrarnos en la potencial capacidad armónica de Phi y sus derivados. La sucesión de Fibonacci y el número de oro son dos caras de la misma moneda.
La sucesión que descubrió el matemático pisano (0,1,1,2,3,5,8,13…) entraría dentro del campo de la aritmética (estudia los números y las operaciones elementales que se pueden realizar con ellos). De esta sucesión deriva el número áureo, representado con la letra griega Phi (Φ,φ) y que sirve para expresar la relación entre dos segmentos de una recta. Es decir, Phi es una construcción geométrica (en relación a las propiedades de las figuras) que surge así:
Phi representado como una línea dividida en dos segmentos a y b, de tal manera que toda la línea (a+b) es al segmento más largo a lo mismo que a es al segmento más corto b φ = (a+b)/ a = a/ b
Si nos valemos del álgebra para obtener el valor numérico de Φ, recurrimos a una ecuación por la cual Φ= a/b. Por lo tanto, aplicado esto a la representación gráfica del segmento anterior: cuando dividimos el total de la longitud del segmento (a+b) entre la parte más larga (a) obtenemos el mismo resultado que al dividir la parte más larga (a) entre la más corta (b). El resultado de esta operación es 1.6180339887… lo que es lo mismo, el número áureo definido por Euclides, “un número infinito e irrepetible” (Mario Livio).
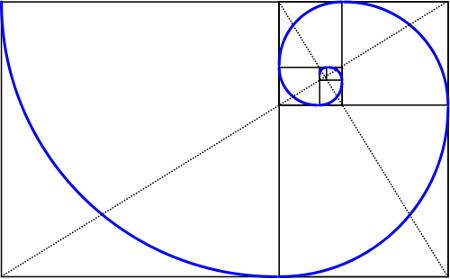
Curiosamente, esta cifra es la misma a la que se aproxima el resultado de dividir cualquiera de los números de la sucesión de Fibonacci entre su antecesor (ejemplo: 5/3= 1.666 ; 13/8=1.625 ). Uniendo estos dos aspectos, es decir, representando mediante la geometría el concepto aritmético, surge una imagen clave para entender por qué este artículo puede fascinarte aunque no seas matemático ni hayas terminado de entender el entramado numérico que hay detrás del descubrimiento de Leonardo el Pisano: la espiral de Fibonnaci.

Reproducción del proceso para formar la espiral de Fibonacci en relación a los números que forman la sucesión (longitud de los rectángulos cuya unión da como resultado el trazado de la propia espiral) Imagen: lamentiraestaahifuera.com
Ubicuidad, ¿ciencia o casualidad?
El número Phi no deja de sorprender con sus propiedades y, al ser descubierto como relación o proporción, ha dado lugar a un amplio análisis de diferentes formas, objetos, representaciones gráficas o incluso patrones de movimiento que tienen lugar en nuestro mundo y que teóricamente están más o menos directamente relacionados con esta proporción, la proporción áurea o divina proporción. El rectángulo áureo o la espiral de Fibonacci, son los ejemplos descritos en este artículo, pero también es posible identificar triángulos áureos o pentágonos áureos. Cualquiera de estas formas se define por tener una propiedad común: respeta la proporción áurea.
Ahora bien, ¿es tan fácil encontrarse con estas formas “áureas” o “divinas” en el entorno que nos rodea? Es decir, más allá de disciplinas como la arquitectura o el diseño, que claramente utilizan las formas y la geometría intencionadamente. ¿Qué pasa con la naturaleza o incluso, con el cosmos? La proporción áurea está en las Pirámides de Egipto, en el logo de Google, en los pétalos de las rosas o en la misma forma de las galaxias. En La Gioconda de Leonardo Da Vinci, en la estructura microscópica de algunos cristales o en las partituras de Debussy. ¿Estamos ante el número más asombroso del mundo? O por el contrario ¿estamos manipulando la realidad queriendo ver matemáticas donde no las hay? Sin duda, después de conocer estos datos tenemos que admitir que las matemáticas tienen una curiosa tendencia a contribuir incluso al conocimiento de materias a las que son, o al menos parecen, totalmente ajenas.
Si quieres profundizar más en la ubicuidad de la proporción áurea y sorprenderte con la variedad de objetos, elementos naturales e incluso las partes del propio cuerpo humano en las que puedes encontrar esta proporción, no te pierdas este artículo en el que analizamos 9 cosas sorprendentemente “condicionadas” por las matemáticas.
